ماراتن نظریه ی اعداد (سطح پیشرفته)
پاسخ : ماراتن نظریه ی اعداد (سطح پیشرفته)
ببخشید. طبق این راه حل یعنی شما ثابت کردین همه اعداد کامل زوج هستند؟؟
خط چهارم واضح نیس .لطفا کمی بیشتر توضیح بدید اگه ممکنه.
اگر
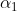 فرد باشد خواهیم داشت :
فرد باشد خواهیم داشت :
 که با توجه به زوج بودن 1+
که با توجه به زوج بودن 1+
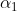 خواهیم داشت
خواهیم داشت
 که با توجه به عبارت بالا میتوان نتیجه گرفت :
که با توجه به عبارت بالا میتوان نتیجه گرفت :
 و چون
و چون
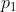 کوچکترین عامل اول n میباشد پس
کوچکترین عامل اول n میباشد پس
 و
و
 که اگر حاصل را در عبارت ابتدایی جاگزین کنیم و پس از کمی ساده کردن خواهیم داشت :
که اگر حاصل را در عبارت ابتدایی جاگزین کنیم و پس از کمی ساده کردن خواهیم داشت :
 که با مقایسه دو طرف این تساوی به سادگی نتیجه میشود که :
که با مقایسه دو طرف این تساوی به سادگی نتیجه میشود که :
 که به سادگی میتوان نتیجه گرفت که این نابرابری به طوراکید جواب ندارد و تنها حالت تساوی میتوان رخ دهد که در این حالت
که به سادگی میتوان نتیجه گرفت که این نابرابری به طوراکید جواب ندارد و تنها حالت تساوی میتوان رخ دهد که در این حالت
 و همچنین در این حالت n نمیتواند عامل اولی غیر از 2 و3 داشته باشد و به عبارتی n=6 که با n>6 در تناقض است و فرض اولیه غلط بوده و
و همچنین در این حالت n نمیتواند عامل اولی غیر از 2 و3 داشته باشد و به عبارتی n=6 که با n>6 در تناقض است و فرض اولیه غلط بوده و
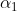 عددی زوج است .
عددی زوج است .
خط چهارم واضح نیس .لطفا کمی بیشتر توضیح بدید اگه ممکنه.
آخرین ویرایش توسط مدیر
- ارسال ها
- 18
- لایک ها
- 13
- امتیاز
- 3
پاسخ : ماراتن نظریه ی اعداد (سطح پیشرفته)
خیر ثابت کرده ام اگر یک عدد کامل شرط گفته شدن در صورت سوال یعنی زوج بودن
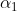 برایش برقرار نباشد اونوقت اون عدد کامل باید زوج باشد . (تو خط سوم راه حل نوشتم این موضوع رو واضح ) در ارتباط خط چهارم هم با توجه به این که:
برایش برقرار نباشد اونوقت اون عدد کامل باید زوج باشد . (تو خط سوم راه حل نوشتم این موضوع رو واضح ) در ارتباط خط چهارم هم با توجه به این که:
 و تساوی نوشته شده در خط اول (با ساده کردن p_i-1 ها از عبارت سمت چپ این تساوی برای i های بزرگتر از 2 ) خواهیم داشت :
و تساوی نوشته شده در خط اول (با ساده کردن p_i-1 ها از عبارت سمت چپ این تساوی برای i های بزرگتر از 2 ) خواهیم داشت :
 و طبق عبارت عاد کردنی که در خط 2 ام راه حل نوشته شده خواهیم داشت :
و طبق عبارت عاد کردنی که در خط 2 ام راه حل نوشته شده خواهیم داشت :
 که این نیز عبارت نوشته شده در خط چهارم را نتیجه میدهد .
که این نیز عبارت نوشته شده در خط چهارم را نتیجه میدهد .
خیر ثابت کرده ام اگر یک عدد کامل شرط گفته شدن در صورت سوال یعنی زوج بودن
- ارسال ها
- 18
- لایک ها
- 13
- امتیاز
- 3
پاسخ : ماراتن نظریه ی اعداد (سطح پیشرفته)
خیر ثابت کرده ام اگر یک عدد کامل شرط گفته شدن در صورت سوال یعنی زوج بودن
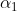 برایش برقرار نباشد اونوقت اون عدد کامل باید زوج باشد . (تو خط سوم راه حل نوشتم این موضوع رو واضح ) در ارتباط خط چهارم هم با توجه به این که:
برایش برقرار نباشد اونوقت اون عدد کامل باید زوج باشد . (تو خط سوم راه حل نوشتم این موضوع رو واضح ) در ارتباط خط چهارم هم با توجه به این که:
 و تساوی نوشته شده در خط اول (با ساده کردن p_i-1 ها از عبارت سمت چپ این تساوی برای i های بزرگتر از 2 ) خواهیم داشت :
و تساوی نوشته شده در خط اول (با ساده کردن p_i-1 ها از عبارت سمت چپ این تساوی برای i های بزرگتر از 2 ) خواهیم داشت :
 و طبق عبارت عاد کردنی که در خط 2 ام راه حل نوشته شده خواهیم داشت :
و طبق عبارت عاد کردنی که در خط 2 ام راه حل نوشته شده خواهیم داشت :
 که این نیز عبارت نوشته شده در خط چهارم را نتیجه میدهد .
که این نیز عبارت نوشته شده در خط چهارم را نتیجه میدهد .
---- دو نوشته به هم متصل شده است ----
در ارتباط با سوالی نیز که قرار داده اید a=b=c=d=2, e=4 در مسئله صدق میکند حالا با ضرب تساوی در یک عدد توان
 ام کامل میتوان بی نهایت جواب طبیعی برای معادله ساخت .
ام کامل میتوان بی نهایت جواب طبیعی برای معادله ساخت .
خیر ثابت کرده ام اگر یک عدد کامل شرط گفته شدن در صورت سوال یعنی زوج بودن
---- دو نوشته به هم متصل شده است ----
در ارتباط با سوالی نیز که قرار داده اید a=b=c=d=2, e=4 در مسئله صدق میکند حالا با ضرب تساوی در یک عدد توان
پاسخ : ماراتن نظریه ی اعداد (سطح پیشرفته)
بله درسته.
البته وقتی شما ثابت کردین که کوچکترین عامل اول باید 2 باشه راه ساده تری هم وجود داشت یعنی از این استفاده کنید عددی کامل و زوج است اگر و تنها اگر به صورت:
) باشد که q و
باشد که q و
 هر دو اول باشند. که دیگه حکم بدیهی میشه.
هر دو اول باشند. که دیگه حکم بدیهی میشه.
خیر ثابت کرده ام اگر یک عدد کامل شرط گفته شدن در صورت سوال یعنی زوج بودن
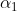 برایش برقرار نباشد اونوقت اون عدد کامل باید زوج باشد . (تو خط سوم راه حل نوشتم این موضوع رو واضح ) در ارتباط خط چهارم هم با توجه به این که:
برایش برقرار نباشد اونوقت اون عدد کامل باید زوج باشد . (تو خط سوم راه حل نوشتم این موضوع رو واضح ) در ارتباط خط چهارم هم با توجه به این که:
 و تساوی نوشته شده در خط اول (با ساده کردن p_i-1 ها از عبارت سمت چپ این تساوی برای i های بزرگتر از 2 ) خواهیم داشت :
و تساوی نوشته شده در خط اول (با ساده کردن p_i-1 ها از عبارت سمت چپ این تساوی برای i های بزرگتر از 2 ) خواهیم داشت :
 و طبق عبارت عاد کردنی که در خط 2 ام راه حل نوشته شده خواهیم داشت :
و طبق عبارت عاد کردنی که در خط 2 ام راه حل نوشته شده خواهیم داشت :
 که این نیز عبارت نوشته شده در خط چهارم را نتیجه میدهد .
که این نیز عبارت نوشته شده در خط چهارم را نتیجه میدهد .
البته وقتی شما ثابت کردین که کوچکترین عامل اول باید 2 باشه راه ساده تری هم وجود داشت یعنی از این استفاده کنید عددی کامل و زوج است اگر و تنها اگر به صورت:
- ارسال ها
- 18
- لایک ها
- 13
- امتیاز
- 3
پاسخ : ماراتن نظریه ی اعداد (سطح پیشرفته)
یعنی شما ثابت کردید که عددی به شکل
) وجود ندارد .(با توجه اول بودن q و
وجود ندارد .(با توجه اول بودن q و
 ) ؟!!! بعد از طرفی عددی به این شکل لزومی ندارد کامل باشد ؟ میشه اگه منظورتون رو اشتباه فهمیدم بیشتر توضیح بدید .
) ؟!!! بعد از طرفی عددی به این شکل لزومی ندارد کامل باشد ؟ میشه اگه منظورتون رو اشتباه فهمیدم بیشتر توضیح بدید .
---- دو نوشته به هم متصل شده است ----
سوال بعدی :تمام اعداد طبیعی k را بیابید که برای ان ها معادله ی زیر بی نهایت جواب a,b,c در اعداد طبیعی داشته باشد .

یعنی شما ثابت کردید که عددی به شکل
---- دو نوشته به هم متصل شده است ----
سوال بعدی :تمام اعداد طبیعی k را بیابید که برای ان ها معادله ی زیر بی نهایت جواب a,b,c در اعداد طبیعی داشته باشد .
- ارسال ها
- 935
- لایک ها
- 1,654
- امتیاز
- 93
پاسخ : ماراتن نظریه ی اعداد (سطح پیشرفته)

اگه که :
 یعنی
یعنی

پس

که واضح هست به ازای هر k بی نهایت جواب داره . پس به ازای هر k بی نهایت جواب (a,b,c) داریم !
سوال بعد :
تمام اعداد گویا m,n,p را بیابید که :
 صحیح شوند
صحیح شوند
یعنی شما ثابت کردید که عددی به شکل
) وجود ندارد .(با توجه اول بودن q و
وجود ندارد .(با توجه اول بودن q و
 ) ؟!!! بعد از طرفی عددی به این شکل لزومی ندارد کامل باشد ؟ میشه اگه منظورتون رو اشتباه فهمیدم بیشتر توضیح بدید .
) ؟!!! بعد از طرفی عددی به این شکل لزومی ندارد کامل باشد ؟ میشه اگه منظورتون رو اشتباه فهمیدم بیشتر توضیح بدید .
---- دو نوشته به هم متصل شده است ----
سوال بعدی :تمام اعداد طبیعی k را بیابید که برای ان ها معادله ی زیر بی نهایت جواب a,b,c در اعداد طبیعی داشته باشد .

---- دو نوشته به هم متصل شده است ----
سوال بعدی :تمام اعداد طبیعی k را بیابید که برای ان ها معادله ی زیر بی نهایت جواب a,b,c در اعداد طبیعی داشته باشد .
اگه که :
پس
که واضح هست به ازای هر k بی نهایت جواب داره . پس به ازای هر k بی نهایت جواب (a,b,c) داریم !
سوال بعد :
تمام اعداد گویا m,n,p را بیابید که :
پاسخ : ماراتن نظریه ی اعداد (سطح پیشرفته)
یعنی شما ثابت کردید که عددی به شکل
) وجود ندارد .(با توجه اول بودن q و
وجود ندارد .(با توجه اول بودن q و
 ) ؟!!! بعد از طرفی عددی به این شکل لزومی ندارد کامل باشد ؟ میشه اگه منظورتون رو اشتباه فهمیدم بیشتر توضیح بدید .
) ؟!!! بعد از طرفی عددی به این شکل لزومی ندارد کامل باشد ؟ میشه اگه منظورتون رو اشتباه فهمیدم بیشتر توضیح بدید .
---- دو نوشته به هم متصل شده است ----
فرض کنید عددی داریم که کامله و زوج هم هست.مثله x در ضمن s فرده:
=\sigma&space;(2^{q-1})\sigma&space;(s)=(2^q-1)\sigma&space;(s))
=s+\frac{s}{2^q-1}) حالا طبق تعریف معلومه که
حالا طبق تعریف معلومه که
 باید 1 باشه یعنی s عددی اوله و حکم ثابت میشه. اونوقت توان 2 که کوچکترین عامل هست زوجه و با فرض اولیه فرد بودن تناقض داره . به غیر از عدد 6...
باید 1 باشه یعنی s عددی اوله و حکم ثابت میشه. اونوقت توان 2 که کوچکترین عامل هست زوجه و با فرض اولیه فرد بودن تناقض داره . به غیر از عدد 6...
---- دو نوشته به هم متصل شده است ----
فرض کنید عددی داریم که کامله و زوج هم هست.مثله x در ضمن s فرده:
پاسخ : ماراتن نظریه ی اعداد (سطح پیشرفته)
فرض می کنیم
 واضح است که
واضح است که
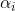 ها فردند. پس فرض می کنیم
ها فردند. پس فرض می کنیم
 که m فرد است. پس داریم(
که m فرد است. پس داریم(
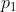 را با p نشان می دهیم):
را با p نشان می دهیم):

اما واضح است که p نمی تواند دو باشد پس j برابر با صفر است که نتیجه می دهد m برابر با یک است. پس داریم:
 که حکم را نتیجه می دهد.
که حکم را نتیجه می دهد.
اينطور كه معلومه يه ١٥ روزي اينجا داره خاك ميخوره
حالا من يه سوال بذارم....
n عددى طبيعى است و مجموع مقسوم عليه هاى مثبت آن توانى از ٢ است ثابت كنيد تعداد اين مقسوم عليه ها هم توانى از ٢ است.
حالا من يه سوال بذارم....
n عددى طبيعى است و مجموع مقسوم عليه هاى مثبت آن توانى از ٢ است ثابت كنيد تعداد اين مقسوم عليه ها هم توانى از ٢ است.
اما واضح است که p نمی تواند دو باشد پس j برابر با صفر است که نتیجه می دهد m برابر با یک است. پس داریم:
پاسخ : ماراتن نظریه ی اعداد (سطح پیشرفته)
فکر میکنم با توجه به قوانین شما باید سوال بعدی رو بذارید . :3:
فرض می کنیم
 واضح است که
واضح است که
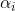 ها فردند. پس فرض می کنیم
ها فردند. پس فرض می کنیم
 که m فرد است. پس داریم(
که m فرد است. پس داریم(
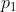 را با p نشان می دهیم):
را با p نشان می دهیم):

اما واضح است که p نمی تواند دو باشد پس j برابر با صفر است که نتیجه می دهد m برابر با یک است. پس داریم:
 که حکم را نتیجه می دهد.
که حکم را نتیجه می دهد.
اما واضح است که p نمی تواند دو باشد پس j برابر با صفر است که نتیجه می دهد m برابر با یک است. پس داریم:
پاسخ : ماراتن نظریه ی اعداد (سطح پیشرفته)
من سابقه ي خوبي توي سوال گذاشتن ندارم يكي دو بار سوال گذاشتم تاپيك خوابيد. اميدوارم اين دفعه اينجوري نشه:
يك عدد صحيح مثبت تناوبي ناميده مي شود اگر در بين هر دو رقم متوالي آن درمبناي 10 يكي زوج و ديگري فرد باشد همه ي اعداد صحيح n را چنان پيدا كنيد كه n مضربي در بين اعداد تناوبي داشته باشد.
فکر میکنم با توجه به قوانین شما باید سوال بعدی رو بذارید . :3:
يك عدد صحيح مثبت تناوبي ناميده مي شود اگر در بين هر دو رقم متوالي آن درمبناي 10 يكي زوج و ديگري فرد باشد همه ي اعداد صحيح n را چنان پيدا كنيد كه n مضربي در بين اعداد تناوبي داشته باشد.
- ارسال ها
- 159
- لایک ها
- 282
- امتیاز
- 0
پاسخ : ماراتن نظریه ی اعداد (سطح پیشرفته)
لم1)دقت کنید که اگر n عددی باشد که نسبت به 10 اول است آنگاه
 به پیمانه n مرتبه ای مانند m دارد.
به پیمانه n مرتبه ای مانند m دارد.
1)ابتدا حالتی بگیرید که n نسبت به 10 اول است. پس به ازای t=2
n|(10101...010)*99

حال فرض کنید تعداد 10 ها در عبارت بالا برابر k باشد. 99k بار 10 رو پشت سرهم بنویسید و اسم این عبارت رو r بگذارید. این عبارت بدیهتا تناوبی است و ثابت میکنیم n|r.
دقت کنید که n|(10101...010)*99=r*99/s کافیست بگوییم s بر 99 بخش پذیر است در این صورت اگر s/99=l آنگاه n|r/l پس n|r اما این نیز طبق لم دو خط بدیهی است(متاسفانه از تایپ این موضوع عاجزم) پس در این حالت مساله حل است.
2)اگر ب. م. م. 100 با n برابر با 10 هم باشد حکم بدیهی است زیرا اثبات کردیم n/10 مضربی تناوبی دارد، و اگر دقت کنید رقم آخر این مضربی که ساختیم صفر است پس این مضرب هم بر n/10 و هم بر 10 بخش پذیر است و چون ب.م.م. 100 با n برابر 10 است پس این دو عدد نسبت به هم اولند پس طبق لم اقلیدس آن مضرب بر n هم بخش پذیر است.
3)حال دقت کنید که اگر n بر 20 بخش پذیر باشد آنگاه بدیهتا n مضرب تناوبی ندارد زیرا رقم آخر همه مضارب n صفر است و رقم ماقبل آخر آنها هم زوج. پس دو رقم زوج متوالی دارند.
پس باید تنها حالاتی را بررسی کنیم که ب. م.م. n با 10 برابر 2 یا 5 است یا n بر 50 بخش پذیر باشد ولی بر 4 بخش پذیر نباشد.
دو حالت اول را میتوان طبق استقرا ثابت کرد که برای توان های 2 و 5 درست است و سپس از لم1 بگوییم در این حالات مضرب تناوبی وجود دارد ، و بخش پذیری n بر 50 را میتوان مانند نتیجه گرفتن پاراگراف 2 از 1 ثابت کرد که مضرب تناوبی وجود دارد پس مضرب تناوبی برای هر n که بر 20 بخش پذیر نیست وجود دارد.
لم1)دقت کنید که اگر n عددی باشد که نسبت به 10 اول است آنگاه
1)ابتدا حالتی بگیرید که n نسبت به 10 اول است. پس به ازای t=2
n|(10101...010)*99
حال فرض کنید تعداد 10 ها در عبارت بالا برابر k باشد. 99k بار 10 رو پشت سرهم بنویسید و اسم این عبارت رو r بگذارید. این عبارت بدیهتا تناوبی است و ثابت میکنیم n|r.
دقت کنید که n|(10101...010)*99=r*99/s کافیست بگوییم s بر 99 بخش پذیر است در این صورت اگر s/99=l آنگاه n|r/l پس n|r اما این نیز طبق لم دو خط بدیهی است(متاسفانه از تایپ این موضوع عاجزم) پس در این حالت مساله حل است.
2)اگر ب. م. م. 100 با n برابر با 10 هم باشد حکم بدیهی است زیرا اثبات کردیم n/10 مضربی تناوبی دارد، و اگر دقت کنید رقم آخر این مضربی که ساختیم صفر است پس این مضرب هم بر n/10 و هم بر 10 بخش پذیر است و چون ب.م.م. 100 با n برابر 10 است پس این دو عدد نسبت به هم اولند پس طبق لم اقلیدس آن مضرب بر n هم بخش پذیر است.
3)حال دقت کنید که اگر n بر 20 بخش پذیر باشد آنگاه بدیهتا n مضرب تناوبی ندارد زیرا رقم آخر همه مضارب n صفر است و رقم ماقبل آخر آنها هم زوج. پس دو رقم زوج متوالی دارند.
پس باید تنها حالاتی را بررسی کنیم که ب. م.م. n با 10 برابر 2 یا 5 است یا n بر 50 بخش پذیر باشد ولی بر 4 بخش پذیر نباشد.
دو حالت اول را میتوان طبق استقرا ثابت کرد که برای توان های 2 و 5 درست است و سپس از لم1 بگوییم در این حالات مضرب تناوبی وجود دارد ، و بخش پذیری n بر 50 را میتوان مانند نتیجه گرفتن پاراگراف 2 از 1 ثابت کرد که مضرب تناوبی وجود دارد پس مضرب تناوبی برای هر n که بر 20 بخش پذیر نیست وجود دارد.
