پاسخ : ماراتن جبر (سطح ممتاز)
نمی دونم راهم درسته یا نه چون از شرط اول هیچ استفاده ای نکردم. پس دنبال جوب باشید! :4:
فرض کنید رابطه ی بالا
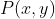 باشه داریم:
باشه داریم:





پس کافیه
 اعداد مثبت رو پیدا کنیم. از طرفی طبق روابط بالا برای
اعداد مثبت رو پیدا کنیم. از طرفی طبق روابط بالا برای
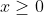 و
و
 دلخواه داریم
دلخواه داریم
 . فرض می کنیم
. فرض می کنیم
 با استفاده از این رابطه داریم:
با استفاده از این رابطه داریم:


 حالا
حالا
 رو به دو طریق حساب می کنیم:
رو به دو طریق حساب می کنیم:


 حالا
حالا
 رو به دو طریق حساب می کنیم:
رو به دو طریق حساب می کنیم:


 با جایگذاری در صورت سوال بدست میاد
با جایگذاری در صورت سوال بدست میاد
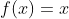 .
.
سوال بعد:همه توابع
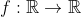 را بیابید به طوری که
را بیابید به طوری که
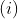 تعداد اعداد حقیقی مانند x که
تعداد اعداد حقیقی مانند x که
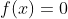 متناهی باشد.
متناهی باشد.
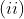
 برای هر x,y حقیقی.
برای هر x,y حقیقی.
فرض کنید رابطه ی بالا


