پاسخ : ماراتن جبر (سطح ممتاز)
فکر کنم جوبش رو بر طرف کردم!
فرض می کنیم برای اعداد
 (این اعداد می تونند متناهی یا نامتناهی باشند و از کوچک به بزرگ مرتب شده اند) داریم
(این اعداد می تونند متناهی یا نامتناهی باشند و از کوچک به بزرگ مرتب شده اند) داریم
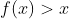 x"> اگه عددی حقیقی مثل
x"> اگه عددی حقیقی مثل
 وجود داشته باشه که برای هر
وجود داشته باشه که برای هر
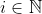 داشته باشیم
داشته باشیم
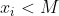 اون وقت می تونیم همون استدلال قبل رو برای اعداد بزرگتر از
اون وقت می تونیم همون استدلال قبل رو برای اعداد بزرگتر از
 انجام بدیم اما اگه این اعداد از بالا کران دار نباشند اون وقت داریم:
انجام بدیم اما اگه این اعداد از بالا کران دار نباشند اون وقت داریم:
 عددی مثل
عددی مثل
 رو طوری در نظر می گیریم که
رو طوری در نظر می گیریم که
 حالا داریم:
حالا داریم:

چون
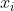 ها از بالا کران دار نیستند اگه
ها از بالا کران دار نیستند اگه
 رو به
رو به
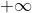 ببریم
ببریم
 به صفر میل می کنه پس
به صفر میل می کنه پس
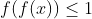 و بقیه ی اثبات مشابه قبله.
و بقیه ی اثبات مشابه قبله.
اگه این دفعه درست بود لطفا خودتون به سوال گذاشتن ادامه بدین! :4:
فکر کنم جوبش رو بر طرف کردم!
فرض می کنیم برای اعداد
اگه این دفعه درست بود لطفا خودتون به سوال گذاشتن ادامه بدین! :4:
